The role of representations to reveal mathematical structures
At Daisy Education, we are committed to supporting educators beyond our online learning programmes. We are thrilled to offer free:
- Teacher resources - to enhance your classroom displays and support your lesson plans.
- CPD events - webinars to help develop your knowledge and practice.
- Initiatives, competitions and challenges - to motivate students and reward success.
We're happy to announce our new series of thought-leadership blogs to further enhance our offerings. Get ready for regular instalments from a range of experts, practitioners and innovators, full of knowledge and expertise in a range of different topics to enrich your classroom.
A huge thank you to John Bee for sharing his insights into...
The role of representations to reveal mathematical structures.
I’ve been talking about the role of representations in maths lessons for over a decade now - but they’re often used poorly: either because a scheme has them already planned, or not at all.
Representing the mathematics we want children to learn supports their thinking and helps them make sense of key concepts. Choosing the right representation to reveal the structure of mathematics is essential. It shapes thinking, communicates ideas and exposes how or why a concept works.
Take a simple example: how might we represent the strategy for calculating 7 + 5? You could reach for a number line or a part–whole model - but these might miss the point entirely.
A number line might encourage a “counting on” strategy, which is efficient but masks the deeper structure. A bar model might be too abstract at this stage. The devil is in the detail. So we must ask: what structure do we want to draw attention to?
Since this calculation can be solved using a bridging through 10 strategy, a tens frame is a better choice. It makes visible how 5 can be decomposed into 3 and 2 to ‘complete the 10’. This rests on a solid understanding of number composition - and helps children see the efficiency behind the method.
As the children gain fluency and mastery of bridging through ten, they can then apply this structure to any calculation that requires this strategy: 9 + 7, 6 + 8, 7 + 5 and so on. The structure can most effectively be revealed using the representation of tens frames.
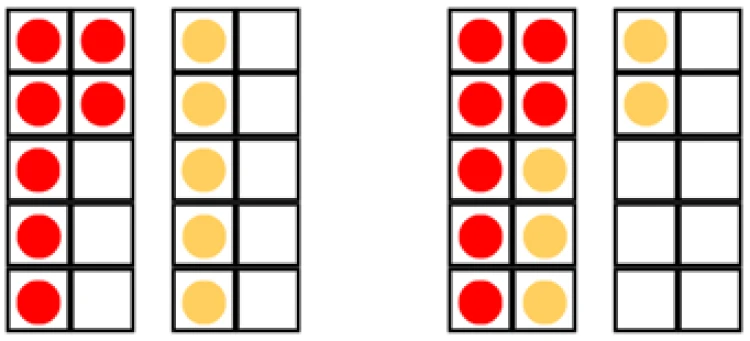
This is an important strategy to master by the end of Key Stage 1. When children arrive in Year 3, they will be introduced to column methods of addition (and subtraction). Suppose a child is presented with the calculation: 237 + 159. A child who is fluent with bridging through ten can calculate the ones column (9 + 7) automatically, whilst a child who is not fluent with this relies on inefficient counting methods and so is doing a harder type of maths.
So, how do we decide which representation to use in class? Many schemes use a wide variety of representations. This, at best, misses the point and, at worst, becomes very confusing for children and busy teachers.
We might ask ourselves:
What structure do I want children to notice?
Not all representations reveal the same things. A number line might show sequencing; a bar model might expose part-whole structure or multiplicative comparison. Think: What relationship or idea do I want to expose?
What prior knowledge do children need to access this representation?
Some representations, like bar models or arrays, are only helpful if the learner already has the necessary schema to interpret them. Otherwise, they become barriers, not bridges.
Does the representation invite generalisation?
A good representation doesn’t just help with this question. It helps children see the underlying pattern they can apply to many questions. It deepens understanding and has a lasting impact on learning.
Can the representation evolve with the concept?
The best tools grow with the learner. Tens frames, for instance, are useful in Year 1 with numbers to 10 and 20, but also reappear in every year group. In upper Key Stage 2 they may be used with decimals (0.7 + 0.5 – bridging strategy may be used here too!).
When we expose mathematical structure, we unlock a world of understanding. The deep structure of many mathematical structures can be applied across the curriculum, including in areas like multiplication.
We know that times tables unlock a world of understanding across the maths curriculum, but which representations are useful? Arrays spring to mind as an obvious choice. However, we may use other representations to reveal other things.
Let us look at the 7 times tables. What do you notice about the way it has been represented?
It may help if we write this out.
1 x 7 = 7
2 x 7 = 14
3 x 7 = 21
4 x 7 = 28
5 x 7 = 35
6 x 7 = 42
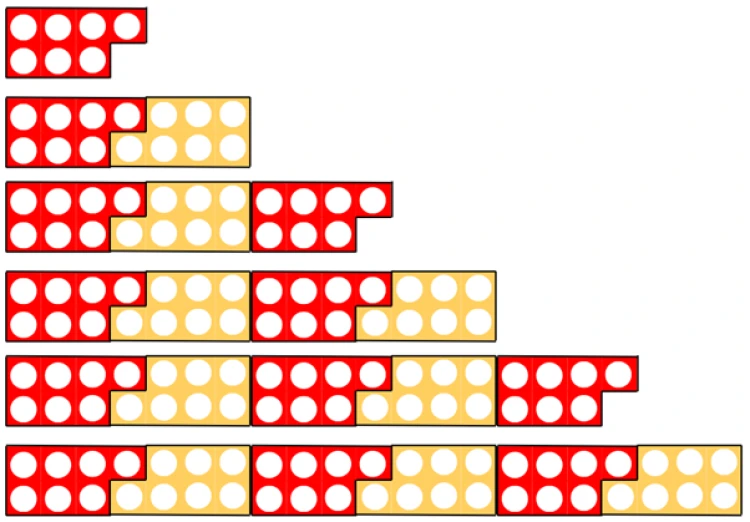
Okay, still not sure what structure it reveals? How about now?

In the left column we can see that odd factor x odd factor = odd product whilst in the right column we can see even factor x odd factor = even product.
Here, the representation exposes that structure and allows children to generalise and ‘see’ the maths. This structure can then be applied to other times tables. In terms of end of Key Stage 2 assessments, it can be a useful self-checking strategy - if children need to calculate 457 x 35, they know that product must be odd due to both factors being odd.
Representations aren’t just tools to ‘help’ children - they are how we reveal the structure of the mathematics itself. When chosen with care, they unlock understanding, support generalisation and build lasting mathematical thinking. But when used without intention, they can confuse, distract, or simply obscure the ideas we’re trying to teach.
So next time you’re planning a lesson, don’t just ask what representation to use - ask why. What structure do I want children to notice? What do I want them to see, connect and remember?
Because when children can see the structure, they can reason with it - and that is where deep, connected learning lives.
John Bee
School Improvement Adviser, Primary Mastery Specialist contributing with the Maths Hubs, and an experienced Headteacher, Deputy Headteacher and Mathematics Leader.
www.mrbeeteach.com

